Scale-Invariant Contour Completion Using Conditional Random Fields
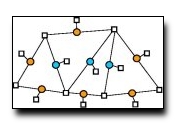
We present a model of curvilinear grouping using piecewise linear
representations of contours and a conditional random field to capture
continuity and the frequency of different junction types. Potential completions
are generated by building a constrained Delaunay triangulation (CDT) over the
set of contours found by a local edge detector.
Maximum likelihood parameters for the model are learned from human labeled
groundtruth. Using held out test data, we measure how the model, by
incorporating continuity structure, improves boundary detection over the local
edge detector. We also compare performance with a baseline local classifier
that operates on pairs of edgels.
Both algorithms consistently dominate the low-level boundary detector at
all thresholds. To our knowledge, this is the first time that curvilinear
continuity has been shown quantitatively useful for a large variety of natural
images. Better boundary detection has immediate application in the problem of
object detection and recognition.
Download: pdf
Text Reference
Xiaofeng Ren, Charless C. Fowlkes, and Jitendra Malik. Scale-invariant contour completion using conditional random fields. In ICCV, II: 1214–1221. 2005.BibTeX Reference
@inproceedings{RenFM_ICCV_2005,AUTHOR = "Ren, Xiaofeng and Fowlkes, Charless C. and Malik, Jitendra",
TITLE = "Scale-Invariant Contour Completion Using Conditional Random Fields",
BOOKTITLE = "ICCV",
YEAR = "2005",
PAGES = "II: 1214-1221",
TAG = "grouping",
BIBSOURCE = "http://www.visionbib.com/bibliography/compute63.html#TT3521"
}