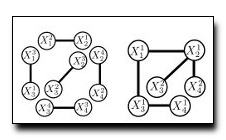
Many computer vision problems involving feature correspondence among images can
be formulated as an assignment problem with a quadratic cost function. Such
problems are computationally infeasible in general but recent advances in
discrete optimization such as tree-reweighted belief propagation (TRW) often
provide high-quality solutions. In this paper, we improve upon these
algorithms in two ways. First, we introduce covering trees, a variant of TRW
which provide the same bounds on the MAP energy as TRW with far fewer
variational parameters. Optimization of these parameters can be carried out
efficiently using either fixed-point iterations (as in TRW) or sub-gradient
based techniques. Second, we introduce a new technique that utilizes bipartite
matching applied to the min-marginals produced with covering trees in order to
compute a tighter lower-bound for the quadratic assignment problem. We apply
this machinery to the problem of finding correspondences with pairwise energy
functions, and demonstrate the resulting hybrid method outperforms TRW alone
and a recent related subproblem decomposition algorithm on benchmark image
correspondence problems.
Download: pdf
Text Reference
Julian Yarkony, Charless Fowlkes, and Alex Ihler.
Covering trees and lower-bounds on quadratic assignment.
In
CVPR. 2010.
BibTeX Reference
@inproceedings{YarkonyFI_CVPR_2010,
AUTHOR = "Yarkony, Julian and Fowlkes, Charless and Ihler, Alex",
TITLE = "Covering Trees and Lower-bounds on Quadratic Assignment",
BOOKTITLE = "CVPR",
YEAR = "2010",
TAG = "grouping"
}